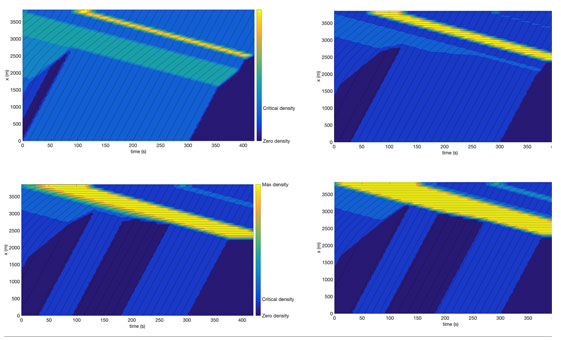
The objective of traffic state estimation is to compute the state of the transportation network from heterogenous sensor data. This problem can be solved using a classical approach, based on variations of Kalman or Particle filtering, or through optimization-based methods.
We currently focus on optimization-based formulations of traffic state estimation based on semi-analytic solutions to the Lighthill Whitham Richards (LWR) model. These semi-analytic solutions allow us to pose the Partial Differential Equation (PDE) model constraints as a set of convex inequalities, which greatly simplifies the problem. We show that this technique can be used to estimate the state of traffic using arbitrary sensors and sensor configurations. The problem of estimating the state of traffic becomes a Linear Program (LP) for boundary data problems, and a Mixed Integer Linear Program (MILP) if some data is located in the interior of the computational domain.
Our present focus is to extend this optimization framework to related problems, including the estimation of traffic state for systems modeled by the hybrid LWR-bounded acceleration model, and the estimation of traffic state with model uncertainty.