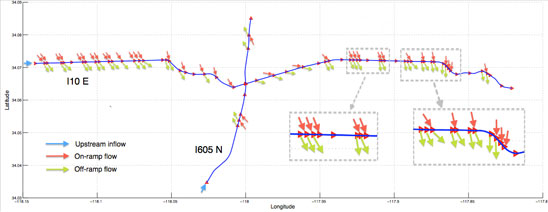
Traffic control consists in modifying the inputs of the transportation systems (boundary demand and supply), or its model parameters (free flow speed, number of lanes) to minimize a cost function.We are currently investigating these two types of control problems.

The first type is boundary control, in which the objective is to modify the demand/supply patterns around a transportation network to minimize a cost function (for example related to delay or congestion level). Using a Hamilton-Jacobi formulation of the LWR model, we show that the problem of controlling a transportation network can be written in general as a MILP (Mixed Integer Linear Program). We are currently extending this framework to robust control problems, in which the initial condition and model parameters are uncertain.

The second type is dynamic speed control, in which the objective is to modify the free flow velocities of highway links to minimize a cost function. We show that such a problem can be efficiently by integrating an optimization loop to a fast forward simulation scheme based on the generalized Lax-Hopf formula. This frast simulation scheme can be used to quickly compute the solution at any point of the transportation network. By integrating this framework within a classical optimization algorithm, we can determine the best controls to apply over a time horizon, to minimize a given objective.