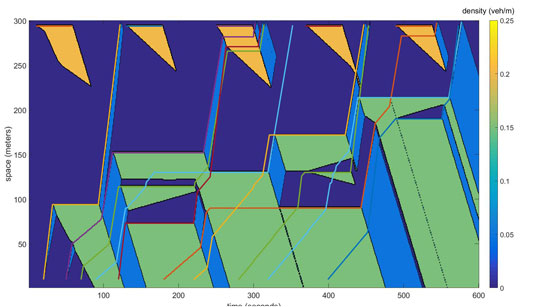
The objective of this project is to investigate new, fast computational methods for solving the Lighthill-Whitham-Richards equation on a homogenous highway link, with an arbitrary number of fixed and moving boundary conditions.

Using semi-analytical methods, we show that the problem can be posed as an hybrid PDE-ODE problem. The parameters of the fixed and moving boundary condtions can be determined efficiently by computing the exact solution to the Hamilton-Jacobi on one dimensional manifolds corresponding to the trajectories of the fixed and moving boundary conditions. Once known, these parameters can be used to compute the solution everywhere on the computational domain, for example using the Lax-Hopf algorithm.